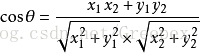基于分词标签的中文短文本相似度

基于分词标签的中文短文本相似度

最近接触到了一些关于中文短文本相似度的算法，将它们总结在此：

• 中文编辑距离
• 基于词频的余弦相似度
• simhash

---

1.0 在相似度算法之前的分词处理

在比较两个字符串 str1 和 str2 之前，我们需要对它们进行分词处理，分词后变成两组标签（我认为分词后的标签具有原子性，不可再分），基于标签，我们可以很容易地进行两组数据的相似度比较。
优点：标签的频率以及相对的位置关系确实一定程度可以表示出重要性和时序关系。
缺点：中文编辑距离（时序关系），余弦相似度（标签重要性）, 他们没有直接的连接。
本项目基于 jieba 分词。

import jieba
str1=jieba.lcut(str1)
str2 = jieba.lcut(str2)

2.1 中文编辑距离

编辑距离，又称 Levenshtein 距离（莱文斯坦距离也叫做 Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作（插入，删除，替换）次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

2.1.1 算法原理

假设我们可以使用 d[i , j] 个步骤（可以使用一个二维数组保存这个值），表示将串 s[ 1…i ] 转换为 串 t [ 1…j ] 所需要的最少步骤个数，那么，在最基本的情况下，即在 i 等于 0 时，也就是说串 s 为空，那么对应的 d[0,j] 就是 增加 j 个字符，使得 s 转化为 t，在 j 等于 0 时，也就是说串 t 为空，那么对应的 d[i,0] 就是 减少 i 个字符，使得 s 转化为 t。

然后我们考虑一般情况，加一点动态规划的想法，我们要想得到将 s[1..i]经过最少次数的增加，删除，或者替换操作就转变为 t[1..j]，那么我们就必须在之前可以以最少次数的增加，删除，或者替换操作，使得现在串 s 和串 t 只需要再做一次操作或者不做就可以完成 s[1..i]到 t[1..j]的转换。所谓的 “之前” 分为下面三种情况：

1. 我们可以在 k 个操作内将 s[1…i] 转换为 t[1…j-1]
2. 我们可以在 k 个操作里面将 s[1..i-1] 转换为 t[1..j]
3. 我们可以在 k 个步骤里面将 s[1…i-1] 转换为 t [1…j-1]

针对第 1 种情况，我们只需要在最后将 t[j] 加上 s[1..i] 就完成了匹配，这样总共就需要 k+1 个操作。

针对第 2 种情况，我们只需要在最后将 s[i] 移除，然后再做这 k 个操作，所以总共需要 k+1 个操作。

针对第 3 种情况，我们只需要在最后将 s[i] 替换为 t[j]，使得满足 s[1..i] == t[1..j]，这样总共也需要 k+1 个操作。而如果在第 3 种情况下，s[i] 刚好等于 t[j]，那我们就可以仅仅使用 k 个操作就完成这个过程。

最后，为了保证得到的操作次数总是最少的，我们可以从上面三种情况中选择消耗最少的一种最为将 s[1..i] 转换为 t[1..j] 所需要的最小操作次数。

2.1.2 代码实现

#其中的str1，str2是分词后的标签列表
def edit_similar(str1,str2):
    len_str1=len(str1)
    len_str2=len(str2)
    taglist=np.zeros((len_str1+1,len_str2+1))
    for a in range(len_str1):
        taglist[a][0]=a
    for a in range(len_str2):
        taglist[0][a] = a
    for i in range(1,len_str1+1):
        for j in range(1,len_str2+1):
            if(str1[i - 1] == str2[j - 1]):
                temp = 0
            else:
                temp = 1
            taglist[i][j] = min(taglist[i - 1][j - 1] + temp, taglist[i][j - 1] + 1, taglist[i - 1][j] + 1)
    return 1-taglist[len_str1][len_str2] / max(len_str1, len_str2)

2.2 基于词频的余弦相似度（TF-IDF）

余弦相似度：计算两者空间向量的夹角来表示两者的相似性。

2.2.1 算法原理

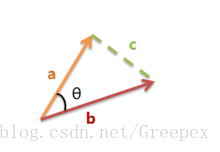
上图是向量 a 和向量 b 以及它们的夹角 θ。根据初等数学公式，假设向量 a、b 的坐标分别为 (x1,y1)、(x2,y2) ，则：

假设 a 是 str1 的标签特征向量，b 是 str2 的标签特征向量，那么两者的相似度可以用 cosθ 表示，且 0<=cosθ<=1。
而关于 str1，str2 的标签特征向量的获取，我们这里用了 TF-IDF 中的思想，利用词频来表示。
例如 str1=[“我”,” 爱”,” 漫威”]，str2=[“我”,” 喜欢”,” 漫威”,” 电影”]
则所有词语的集合为 [“我”,” 爱”,”喜欢”,”漫威”,”电影”]
str1（计算相应词频）转变后的 a=[1,1,0,1,0]
str2（计算相应词频）转变后的 b=[1,0,1,1,1]
计算后的相似度为：0.577350

2.2.2 代码实现

#其中的str1，str2是分词后的标签列表
def cos_sim(str1, str2):
    co_str1 = (Counter(str1))
    co_str2 = (Counter(str2))
    p_str1 = []
    p_str2 = []
    for temp in set(str1 + str2):
        p_str1.append(co_str1[temp])
        p_str2.append(co_str2[temp])
    p_str1 = np.array(p_str1)
    p_str2 = np.array(p_str2)
    return p_str1.dot(p_str2) / (np.sqrt(p_str1.dot(p_str1)) * np.sqrt(p_str2.dot(p_str2)))

2.3 simhash

simhash 是一种 hash 算法，以前在我印象中 hash 算法是将一个对象映射成一个 hash 值，一般只要求当两个对象完全相同时才有相同的 hash 值，而两个相似的对象的 hash 值并不需要有任何关系。只相差一个字符 hash 出来的值也可能相差十万八千里。但是如果 hash 函数设计的足够巧妙，也可以让相似的对象拥有相同或者相似的 hash 值，使用 hash 来进行相似性搜索更方便快捷。
simhash 就是这么一个神奇的算法。它满足：

• 当两个对象的距离不大于 d1 时，它们的 hash 值相同的概率不小于 p1，即如 d(x, y) ≤ d1，则 P(hash(x) = hash(y)) ≥ p1.
• 当两个对象的距离不小于 d2 时，它们的 hash 值相同的概率不大于 p2，即如 d(x, y) ≥ d2，则 P(hash(x) = hash(y)) ≥ p2.

simhash 可以将文档 hash 到一个 64 位二进制数，使得相似的文档具有相似的二进制数。对于一个文档，我们可以把文中的每个词或者词组作为一个特征，统计各个特征出现的频率（当然也可以加入词性的权重，怎么去设置、统计特征可以视情况而定）。下面的例子中我们使用 jieba 做分词。

目标文档 “葫芦娃葫芦娃，一根藤上七朵花”，得到的特征与相应的频率：（葫芦娃，0.33），（一根，0.17，（藤上，0.17），（七朵，0.17），（花，0.17）。然后对特征值进行 hash，方便演示这里映射到 6 位：

• 葫芦娃：100100
• 一根：010101
• 藤上：101010
• 七朵：111010
• 花：001010
  然后根据二进制数的各个二进制位，我们队每个特征构造一个向量。如果一个特征映射到的二进制数的某一位是 1，则其向量对应位置上的分量为该特征的频率，否则为频率的相反数。如：
  葫芦娃：（0.33，-0.33，-0.33，0.33，-0.33，-0.33）
  ……
  将向量相加，得到（0.33，-0.33，0，0，0，-0.66）
  对于每个分量，如果大于 0 就取 1，否则取 0，这样就能得到二进制数的 simhash，即 100000。

在文本中，出现频率高的特征，其对应的向量分量的绝对值更大，对最终向量相加的结果影响也更大。因此，如果两个文档相似，那么它们出现频率高的特征也应该比较接近，最终得到的 hash 值也就越接近。在 google 网页的检索中，64 位 hash 中至多有 3 个二进制位不同可判定为相似文档。

2.3.1 代码实现

def simhash(cls, s, RE=None, cut_func=None):
  if RE:
     REX = RE
 else:
    REX = re.compile(u'[\u4e00-\u9fa5]+')
  if not cut_func:
    cut_func = cls.cut_func
  cut = [x for x in cut_func(s) if re.match(REX, x)]
  ver = [[v * (int(x) if int(x) > 0 else -1) for x in k] for k, v in cls.hist(cut).items()]
  ver = np.array(ver)
  ver_sum = ver.sum(axis=0)
  sim = ''.join(['1' if x > 0 else '0' for x in ver_sum])
  return sim

首先我们用正则定义了感兴趣的区域，这里我们只取我们感兴趣的中文。然后我们定义了分词所用的函数，这里使用的是 jieba 分词。
然后我们得到分词的结果：

cut = [x for x in cut_func(s) if re.match(REX, x)]

得到向量矩阵：

ver = [[v * (int(x) if int(x) > 0 else -1) for x in k] for k, v in cls.hist(cut).items()]

为了方便计算我们引入 numpy 帮我们做矩阵计算：

ver = np.array(ver)
ver_sum = ver.sum(axis=0)

最后将计算结果转换为二级制 hash。因为我们这里使用的 32 位 md5 给分词结果做的 hash 所以最后得到的 hash 值也是 32 位的：

11111101011001101110111100101101

其中我们用到了几个工具函数：

@classmethoddef
hist(cls, cut):
  _cut = {x: 0 for x in set(cut)}
  for i in cut:
    _cut[i] += 1
  return {cls.hash_bin(k): v/len(cut) for k, v in _cut.items()}

hist 函数是将分词列表转换为特征频率向量的。

@classmethoddef
hash2bin(cls, hash):
  d = ''
  for i in hash:
  try:
    if int(i) > 7:
      d = d + '1'
    else:
      d = d + '0'
    except ValueError:
      d = d + '1'
    return d
@classmethoddef
hash_bin(cls, s):
  h = hashlib.md5(s.encode()).hexdigest()
  return cls.hash2bin(h)

其中 hash_bin 函数用来将字符 Hash 成二级制 hash 值，基础 hash 算法为 32 位 md5。
hash2bin 函数是将 16 进制 hash 值映射成二进制 hash。
为了方便比较我们使用海明距离来判定两个 hash 值的相似度：

@staticmethoddef
haiming(s1, s2):
  x = 0
  for i in zip(s1, s2):
    if i[0] != i[1]:
      x += 1
return x

---

效果

1993 年，南京大学有这样一个男生寝室，四个男生都没有女朋友，于是搞了个组合叫 “名草无主四大天王”。这四大天王坚持每晚举行“卧谈会”，从各种学术上讨论如何摆脱光棍状态。这一年的 11 月，校园的梧桐树落叶凋零，令他们分外伤情。他们在 11 日这一天晚上卧谈时，符号学的灵感突然登门造访。11 月 11 日，四个 1 字排开，不正是好像四根光秃秃的棍子吗？这四根光棍不正是在巧妙地诉说着“名草无名四大天王” 的凄凉吗？

工信部回应“4G 降速”传闻：工信部绝不会下达降低 4G 速率的指令

以上是一片文章中的节选。
两个的 simhash 是
11111101011001101110111100101101
00101101001010110001100000101110
海明距离为 16。

工信部回应“4G 降速”：绝不会下达降低 4G 速率的指令

这段是第二段稍加修改，simhash 为：
00100101001010110000100000101110

与第二段的海明距离为 2
可以看出效果还是很明显的。

---

能序列化的东西都能 hash，也就都能比较相似度。simhash 属于局部敏感哈希（Local-Sensitive Hashing, LSH），下次讲讲如何比较图片的相似度，使用感知哈希（Perceptual Hashing)。