一、背景
用户可以通过视频更全面直观的展示商品,于此同时也出现了一些视频拷贝、抄袭等不好的现象。为了解决这个问题,我们采用了很多方案,其中一种方案是将商品视频转换成向量,尝试通过向量检索计算商品视频相似性,进而判断商品是否重复。
视频去重本质是高维向量检索,基于当前商品规模及业务发展的预估,向量检索系统需支持检索亿级别平均时长为 20 秒,每秒向量维度是 1024 维的视频。如此庞大的量级给我们的技术选型和实现带来了一定的挑战。
二、挑战
向量检索系统的挑战主要在几个方面:
数据量大 商品的视频总帧数在亿级别;
单帧维度高 为保证向量召回的准确率,目前单帧向量维度是 1024 维;
高精度召回 为保证效果,向量召回的准确率在 95% 以上;
高性能 为保证用户体验,单帧单次召回耗时 100ms 左右,QPS 在 1000 以上。
高维向量检索需要解决在数据维度增加之后导致检索性能急剧下降的问题。高维向量数据的特点主要包括以下三个方面:
稀疏性。随着维度增长,数据在空间分布的稀疏性增强;
空空间现象。对于服从正态分布的数据集,当维数大约增加到 10 时,只有不到 1%的数据点分布在中心附近;
维度效应。随着维数的增加,对索引的维护效率急剧下降,并且高维空间中数据点之间的距离接近于相等。
三、实现方案
基于上述的业务背景及挑战,我们从以下几个方面重新梳理了相关实现。
3.1 视频向量化
向量化是指将视频数据按照一定的算法转换为向量进行表示,转换算法决定了向量表达原始视频数据的准确性。向量化使得对视频数据的检索、去重、计算相似性等操作转化为对向量的求距离或求夹角操作。
视频向量化即在视频中抽取关键帧,对每帧视频进行特征提取,包含局部特征提取和全局特征提取。局部特征提取包含 “特征点检测”、“特征点描述”、“特征描述降维”。全局特征提取同样包含多个步骤,我们将这些步骤封装为自定义算子,利用 Tensorflow Lite 模型将自定义算子组合起来,这样就可以动态更新算子,达到算法实时更新的目的。
将视频转化为向量之后,计算视频的相似性就相当于计算向量的相似性。计算向量相似性有几种方式,分别为计算海明距离、夹角余弦、欧式距离和向量内积等。
3.2 计算向量距离
3.2.0 欧式距离
欧式距离全称是欧几里距离,是最易于理解的一种距离计算方式,源自欧式空间中两点间的距离公式。它以经过人们一致评价的物品为坐标轴,然后将参与评价的人绘制到坐标系上,并计算他们彼此之间的直线距离。


图中用户 A 和用户 B 分别对项目 X、Y 进行了评分。用户 A 对项目 X 的评分为 2,对项目 Y 的评分为 4,表示到坐标系中为坐标点 A(1.8, 4);同样用户 B 对项目 X、Y 的评分表示为坐标点 B(4.5, 2.5),因此他们之间的欧几里德距离(直线距离)为:sqrt((B.x - A.x)^2 + (A.y - B.y)^2)

计算出来的欧几里德距离是一个大于 0 的数,为了使其更能体现用户之间的相似度,可以把它规约到 (0, 1] 之间,具体做法为:1 / (1 + d)。参见 Table2

只要至少有一个共同评分项,就能用欧几里德距离计算相似度;如果没有共同评分项,那么欧几里德距离也就失去了作用。其实照常理理解,如果没有共同评分项,那么意味着这两个用户或物品根本不相似。
二维的公式
d = sqrt((x1-x2)^2+(y1-y2)^2)
平面空间内的 与
间的欧式距离:
三维的公式
d=sqrt(x1-x2)^2+(y1-y2)^2+(z1-z2)^2)
推广到 n 维空间,
Python 代码简单实现:
1 | def EuclideanDistance(x,y): |
使用 numpy 简化:
1 | import numpy as np |
3.2.1 海明距离
严格来说,海明距离其实和向量没有太大关系,海明距离计算的是两个等长字符串对应位置字符不同的个数。换句话说,海明距离表示将一个字符串变换成另一个字符串所需要替换的字符个数。 对于向量来说,海明距离可以看作是将一个向量变换成另一个向量所需要替换的坐标个数。
0100→1001 海明距离是 3; 0110→1110 海明距离是 1
3.2.2 向量夹角余弦
计算向量的 cos 夹角即在坐标系中,向量从原点出发,分别指向不同的方向,计算两个方向之间夹角。若两个向量之间夹角越小则向量越相似。
在二维空间中,向量 A 的坐标是 [x1,y1],向量 B 的坐标是 [x2,y2]。向量 A 和 B 之间夹角余弦公式为
同样夹角余弦公式对多维向量也成立,假设想 A 和 B 的坐标分别是 [A1,A2,…,An]、[B1,B2,…,Bn],则 A 与 B 之间夹角 θ 余弦公式为:
夹角 θ 余弦越接近 1 标示夹角越接近 0 度,即两个向量越相似,这就是通过计算向量夹角来确定向量相似性的方法。
首先,样本数据的夹角余弦并不是真正几何意义上的夹角余弦,只不过是借了它的名字,实际是借用了它的概念变成了是代数意义上的 “夹角余弦”,用来衡量样本向量间的差异。
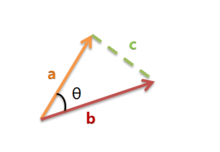
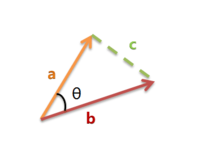 几何意义上的夹角余弦
几何意义上的夹角余弦
夹角越小,余弦值越接近于 1,反之则趋于 - 1。我们假设有 x1 与 x2 两个向量:
Python 代码的简单按公式还原:
1 | def Cosine(x,y): |
使用 numpy 简化夹角余弦
1 | def Cosine(dataA,dataB): |
我们引入一组特殊数据进行测试:
1 | dataA = np.mat([1,2,3,3,2,1]) |
欧式距离和夹角余弦的区别:
对比以上的结果的 dataA 与 dataB 这两组数据,会发现 dataA 与 dataB 的欧式距离相似度比较小,而夹角余弦相似度比较大,即夹角余弦更能反映两者之间的变动趋势,两者有很高的变化趋势相似度,而欧式距离较大是因为两者数值有很大的区别,即两者拥有很高的数值差异。
3.2.3 向量欧式距离
向量欧式距离即向量顶点之间的距离,在 N 维空间中两点 x1 和 x2 之间的距离公式:
欧式距离越小表示向量的顶点之间越近,即向量之间更相似。
3.1.4 向量内积
通过公式可以发现向量内积与向量夹角余弦的含义类似,内积与夹角余弦成正比,内积越大,夹角余弦越大,夹角越小。
不同的距离计算公式反应的是向量不同维度的特征,需要根据向量生成算法选择距离计算公式。我们对上面几种公式进行了召回率测试,测试结果(计算公式与召回率关系)见下表。
3.1.5 皮尔逊相关系数
假如之不先介绍夹角余弦的话,第一次接触你绝对会对皮尔逊相关系数一脸懵逼。那么现在,让我们再来理解一下皮尔逊相关系数的公式:
- 这里减去的
每个 item 被打分的均值
皮尔逊相关系数公式实际上就是在计算夹角余弦之前将两个向量减去各个样本的平均值,达到中心化的目的。从知友的回答可以明白,皮尔逊相关函数是余弦相似度在维度缺失上面的一种改进方法。
1.Python 代码实现皮尔逊相关系数:
1 | def Pearson(x,y): |
- numpy 简化实现皮尔逊相关系数
1 | def Pearson(dataA,dataB): |
用余弦相似度相同的方法实现皮尔逊:
1 | # 余弦相似度、修正余弦相似度、皮尔逊相关系数的关系 |
3.1.5 汉明距离
汉明距离表示的是两个字符串(相同长度)对应位不同的数量。比如有两个等长的字符串 str1 = “11111” 和 str2 = “10001” 那么它们之间的汉明距离就是 3(这样说就简单多了吧。哈哈)。汉明距离多用于图像像素的匹配(同图搜索)。
1.Python 的矩阵汉明距离简单运用:
1 | def hammingDistance(dataA,dataB): |
3.1.5 曼哈顿距离
没错,你也是会曼哈顿计量法的人了,现在开始你和秦风只差一张刘昊然的脸了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,那么驾驶的最近距离并不是直线距离,因为你不可能横穿房屋。所以,曼哈顿距离表示的就是你的实际驾驶距离,即两个点在标准坐标系上的绝对轴距总和。
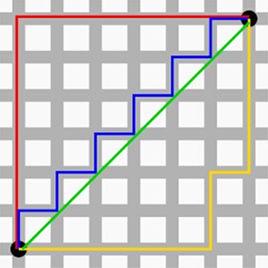
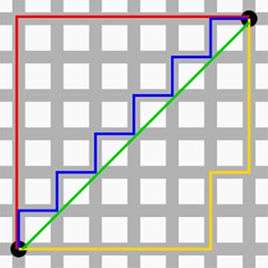 曼哈顿距离
曼哈顿距离
1 | # 曼哈顿距离(Manhattan Distance) |
3.3 向量检索
对于向量检索来说,通常有三类方法:基于树的方法、hash 方法、矢量量化方法,每种方法都有各自的适用范围。
3.3.1 基于树的方法
KD 树是其下的经典算法。一般而言,在空间维度比较低时,KD 树的查找性能还是比较高效的;但当向量维度较高时,该方法会退化为暴力枚举,性能比较差,这时一般会采用下面的哈希方法或者矢量量化方法。
一个三维 k-d 树。第一次划分(红色)把根节点(白色)划分成两个节点,然后它们分别再次被划分(绿色)为两个子节点。最后这四个子节点的每一个都被划分(蓝色)为两个子节点。因为没有更进一步的划分,最后得到的八个节点称为叶子节点。
3.3.2 hash 方法
LSH(Locality-Sensitive Hashing) 是 hash 方法的代表算法。它是用 hash 的方法把数据从原空间哈希到一个新的空间中,使得在原始空间的相似的数据,在新的空间中也相似的概率很大,而在原始空间的不相似的数据,在新的空间中相似的概率很小。
对于小数据集和中规模的数据集 (几个 million - 几十个 million),基于 LSH 的方法的效果和性能都很不错。这方面有 2 个开源工具 FALCONN 和 NMSLIB。
3.3.3 矢量量化方法
矢量量化方法,即 vector quantization。矢量量化常用于数据压缩,是将一个向量空间中的点用其中的一个有限子集来进行编码的过程。并用聚类后的中心点的标签替代该簇中其他点的标签,以此达到缩小子集大小,压缩数据的目的。
所以矢量量化方法天生就适合做大数据集处理,在本次项目中我们也使用矢量量化方法处理闲鱼商品视频的超大数据集,缩小检索规模,在保持较高检索准确率的同时大幅度提高检索性能。
在矢量量化编码中,关键是码本的建立和码字搜索算法。比如常见的层次聚类算法,就是一种矢量量化方法。而在相似搜索中,向量量化方法又以 PQ 方法最为典型。
3.3.3.1 层次聚类算法(HC)
层次聚类 (Hierarchical Clustering) 是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。
在超大数据规模,同时要求高准确率情况下,可以通过多层聚类的方法,通过中心点来表示候选集,从而降低触达候选集的计算量。在保证结果的同时,大幅加快计算速度。
3.3.3.2 乘积量化算法(PQ)
乘积量化即 Product Quantization,这里的乘积是指笛卡尔积(Cartesian product),意思是指把原来的向量空间分解为若干个低维向量空间的笛卡尔积,并对分解得到的低维向量空间分别做量化(quantization)。这样每个向量就能由多个低维空间的量化 code 组合表示。
PQ 是一种量化(quantization)方法,本质上是数据的一种压缩表达方法,所以该方法除了可以用在相似搜索外,还可以用于模型压缩,特别是深度神经网络的模型压缩上。
PQ 算法可以理解为是对 vector quantization 做了一次分治,首先把原始的向量空间分解为 m 个低维向量空间的笛卡尔积,并对分解得到的低维向量空间分别做量化,那如何对低维向量空间做量化呢?恰巧又正是用 kmeans 算法。所以换句话描述就是,把原始 D 维向量(比如 D=128)分成 m 组(比如 m=4),每组就是
,各自用 kmeans 算法学习到一个码本,然后这些码本的笛卡尔积就是原始 D 维向量对应的码本。
可以看到 m=1 或者 m=D 是 PQ 算法的 2 种极端情况,对 m=1,PQ 算法就回退到 vector quantization,对 m=D,PQ 算法相当于对原始向量的每一维都用 kmeans 算出码本。
图 2 是在这个默认配置下对 128 维的原始数据用 PQ 算法的示意图。
根据上面的介绍,我们主要对矢量量化方法进行测试,对引擎支持的 HC 和 PQ 算法进行测试,测试向量规模:760w、维度:65、距离计算方法: 内积、向量类型:float,测试结果如下:
从测试结果来看,HC 算法的召回率和延时比 PQ 算法要好一些,但因为闲鱼视频是高维度的向量数据集,PQ 算法的表现更稳定,所以我们最终选用的是 PQ 算法实现向量检索。
3.4 项目架构
上面说的是本次项目应用到的算法知识,这一章节主要阐述项目整体架构。
3.4.1 应用架构
应用架构分为几个部分:
客户端
闲鱼客户端在 TensorFlow Lite 的基础上定制开发了算法容器,实现在端上将视频提取关键帧,对单帧视频进行视频特征计算;根据在端上计算的特征,在云上检索视频向量库,检索相似向量,最后计算出相似视频。
微服务集群
后端封装通用向量统一接入层,屏蔽底层对接不同向量检索引擎对上层的影响,并且预留扩展点,为后续接入图片向量和商品向量打下基础。后端接收到视频向量后调用底层向量检索引擎召回相似结果,并根据商品状态过滤、重新计算视频相似分;后端会将视频向量数据保存到日志中,由日志监听同步系统将向量数据同步到离线数据中心。
日志监听同步系统
日志监听同步系统会实时监听指定日志文件变化,并根据指定格式解析日志数据,将解析后的数据同步到离线数据中心。
离线数据中心
离线数据中心每 15 分钟生成一个实时增量视频向量数据的分区,每天会对昨日全量数据和当日增量数据做合并,再将合并后的当日全量数据回流到向量检索引擎,构建当日全量数据的索引。
向量检索引擎
我们本次使用的向量检索引擎是阿里内部自研的 BE,BE 是阿里推荐系统负责在线召回的引擎,向量召回是 BE 最新集成的召回策略,融合了搜索从离线到在线的全链路技术体系,并依托强大的管控系统,实现了从开发、上线到运维的全生命周期管理。
BE 从逻辑上来说,主要负责从多种类型的索引表中召回数据并关联具体的业务信息进行过滤和粗排。其中 filter 和 sorter 是算法插件,可以灵活配置在检索流程的各个环节,具体的过滤和排序逻辑由算法同学根据业务场景进行编写,同时 BE 也内置了大量的通用组件。 BE 引擎维护向量数据索引,对外提供向量检索服务,并且会定时从离线数据中心同步向量数据构建索引。
BE 引擎深度集成开源的 KNN 库–FAISS,改造定制使其支持向量索引的分布式构建和查询,实现多种基于量化的方法如粗量化、积量化以及粗量化 + 积量化的组合等方法,并且在线查询的延时、索引构建的性能都很优秀。
3.5 上线效果
通过向量检索方法进行视频去重,通过定制计算向量算法、适配向量内积计算方法和 PQ 算法优化等方式,上线之后,经过闲鱼线上超大商品视频数据集验证之后,整个系统 QPS 在 1000 以上,召回延时在毫秒级别,视频去重整体延时在 100 毫秒左右;视频召回率最终稳定在 95% 以上。
四、总结
本文主要介绍闲鱼如何使用向量检索方法实现视频去重业务,描述了视频去重的业务背景、向量检索涉及的相关算法及视频去重的应用架构,希望给各位读者带来一些思考和启发。 项目一期首先实现了在闲鱼视频上的去重能力,我们会继续将去重、搜索能力应用到商品图片甚至是商品本身,后续会继续和大家分享,敬请期待。
闲鱼技术团队是一只短小精悍的工程技术团队。我们不仅关注于业务问题的有效解决,同时我们在推动打破技术栈分工限制(android/iOS/Html5/Server 编程模型和语言的统一)、计算机视觉技术在移动终端上的前沿实践工作。作为闲鱼技术团队的软件工程师,您有机会去展示您所有的才能和勇气,在整个产品的演进和用户问题解决中证明技术发展是改变生活方式的动力。
简历投递:guicai.gxy@alibaba-inc.com
五、参考资料
PQ 算法
faiss
Large-scale video retrieval using image queries
https://lear.inrialpes.fr/pubs/2011/JDS11/jegousearchingwith_quantization.pdf